

样例输入
1 | 3 4 2 |
样例输出
1 | 2 |

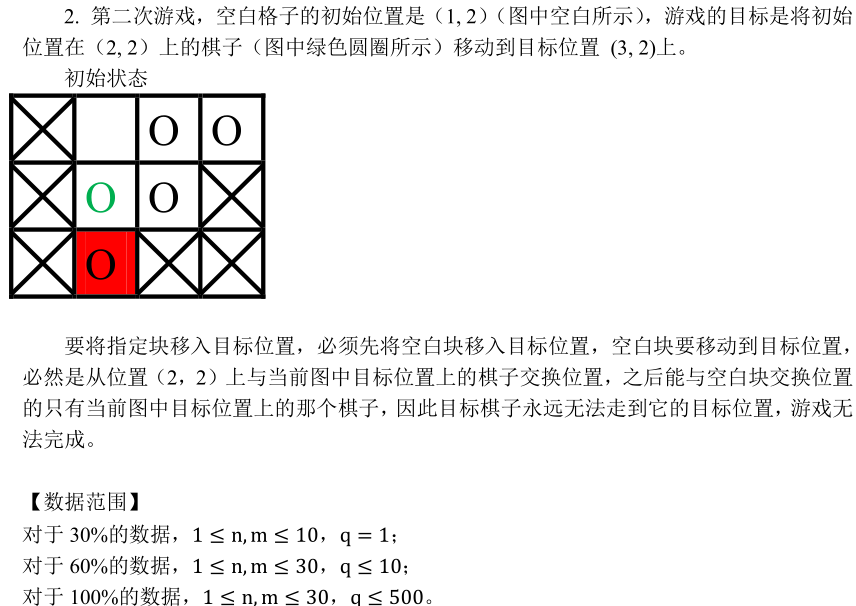
题解
算法分析摘自《2013全国信息学奥林匹克年鉴》
算法分析
这道题主要考察同学们对最短路算法的理解。(我考试的时候怎么没看出来orz)
本题是一个很典型的最短路模型的题目。
假设我们把棋盘的局面当作结点,若A局面能通过一步变成B局面则将A局面和B局面对应的结点连上一条边权为1的边。那么问题就成了求这样建成的图中从初始局面对应的结点到达指定移动格在目标位置的局面对应的那些结点的最短路。也就是求边权都为1的途中的一个单源最短路,用BFS就可以解决这个问题了。具体做法如下:
用(EX,EY,MX,MY)表示空白格在(EX,EY),指定移动格在(MX,MY)的局面所对应的结点。
- 将(EX,EY,SX,SY)进队,将Distance(EX,EY,SX,SY)设为0。
- 若队为空,则输出无解,算法结束。
- 将队首元素取出,设为(EX,EY,MX,MY)。
- 若(MX,MY)等于(TX,TY),则Distance(EX,EY,MX,MY)即为所求答案,算法结束。
- 否则,设由(EX,EY,MX,MY)能到达的局面(EX’,EY’,MX’,MY’),且(EX’,EY’,MX’,MY’)从未进队过,则将(EX’,EY’,MX’,MY’)进队,将Distance(EX’,EY’,MX’,MY’)设Distance(EX,EY,MX,MY)+1,然后跳至步骤2.
可以知道,一个局面由空白格的位置和指定移动格的位置唯一确定,所以局面的数量是$O((nm)^2)$的,也就是说建成的图的结点数是$O((nm)^2)$的。由于每个局面只可能通过空格和上下左右的移动格交换来变成另外一个局面,所以建成的图中的边数也是$O((nm)^2)$的。因此求一次最短路的时间复杂度就为$O(V+E)$,即$O((nm)^2)$。但是询问有q次,所以总的时间复杂度为$O(q(nm)^2)$。
我们发现之间bfs不能满足题目的要求,所以算法还需要优化。
进一步分析可以发现,指定移动格只有当空白格在它附近才能移动,所以游戏的过程可以看成将空白格先移动到指定移动格附近(此处不考虑初始位置和目标位置相同的情况),然后指定移动格和空白格交换,再将空白格移动到指定移动格附近,然后再将空白格移动到指定移动格附近,然后再将指定移动格和空白格交换……如此循环下去,直至指定移动格达到目标位置。
如果只考虑空白格在指定移动格附近的局面,那这样的局面数显然是$O(nm)$的。而局面之间的转移我们只考虑两种,一种是交换指定移动格附近的位置(比如由上方移动到右方)。第一种转移只需要一步,而第二种转移所需的步数就等于固定指定移动格后将空白格移动所需的最小步数,这个步数可以bfs求出,且由于这样的bfs只有$O(nm)$种,且每种所需的时间是$O(nm)$,所以我们可以在$O((nm)^2)$的时间内预处理出来(或者像标程一样采用记忆化的方法)。
两种转移总共最多能转移到5个新的局面,所以暗张这样的局面来建图,点数和边数都是$O(nm)$的,但是边权就不是全为1了,所以需要用dijsktra算法来求最短路,时间复杂度为$O(nm\times log(nm))$。加上预处理,总的时间复杂度为$O((nm)^2+nm\times log(nm))$
至此,本题就完美地解决了。
代码
代码来自@ghj12221
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
using namespace std;
//方向数组
const int dx[] = {0, 0, 1, -1}, dy[] = {1, -1, 0, 0};
//mp是读入的地图,tt[i][j][d1][d2]是不经过(i,j)的情况下,(i,j)的d1方向转移到 (i,j)的d2方向的最短距离
//d是广搜求距离用到的d数组,di是dijkstra时用到的d数组 v是dijkstra时用到的标记数组
int mp[32][32], tt[32][32][4][4], d[32][32], di[32][32][4];
bool v[32][32][4];
int n, m, q;//如题
//dijkstra过程中用到的状态结构体
struct st
{
int x, y, d, dis;
st(int x = 0, int y = 0, int d = 0, int dis = 0) : x(x), y(y), d(d), dis(dis)
{
//构造函数
}
friend bool operator>(const st &a, const st &b);
};
//获取当前方向与dir相反的方向
int rev(int dir)
{
// printf("(%d,%d) - > (%d,%d)\n", dx[dir], dy[dir], dx[dir ^ 1], dy[dir ^ 1]);
return dir ^ 1;
}
//因为要使用小根堆,所以这里重载了大于号
bool operator>(const st &a, const st &b)
{
return a.dis > b.dis;
}
//判断一个点是否合法(是否能够走到)
bool valid(int x, int y)
{
return x >= 1 && x <= n && y >= 1 && y <= m && mp[x][y] == 1;
}
//利用bfs算法求出(x1,y1)到(x2,y2)的距离
int dis(int x1, int y1, int x2, int y2)
{
// printf("求出(%d,%d)到(%d,%d)的距离\n", x1, y1, x2, y2);
if(x1 == x2 && y1 == y2)
return 0;
memset(d, 0x3f, sizeof(d));
queue<int> qx, qy;//队列
qx.push(x1);
qy.push(y1);
d[x1][y1] = 0;
while (!qx.empty())
{
int x = qx.front(), y = qy.front();
qx.pop();
qy.pop();
for (int i = 0; i <= 3; i++)
{
int nx = x + dx[i], ny = y + dy[i];
if(valid(nx, ny) && d[nx][ny] >= inf)//当前方块合法且没有被搜索
{
d[nx][ny] = d[x][y] + 1;
if(nx == x2 && ny == y2)//到了终点
{
// printf("(%d,%d)到(%d,%d)的距离为%d\n", x1, y1, x2, y2, d[nx][ny]);
return d[nx][ny];
}
qx.push(nx);
qy.push(ny);
}
}
}
return inf;
}
void prework()
{
int x1, y1, x2, y2;
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
if (mp[i][j] == 1)
{
mp[i][j] = 0;//暂时将(i,j)标记为不可以动的方块
for (int src = 0; src <= 3; src++)//枚举d1
if (valid(x1 = i + dx[src], y1 = j + dy[src]))//d1方向的块合法
for (int dest = 0; dest <= 3; dest++)//枚举d2
if (valid(x2 = i + dx[dest], y2 = j + dy[dest]))//d2方向的块合法
tt[i][j][src][dest] = dis(x1, y1, x2, y2);//求两个块间的距离
mp[i][j] = 1;//还原标记
}
}
void work()
{
int ex, ey, sx, sy, tx, ty;//如题
priority_queue<st, vector<st>, greater<st> >pq;//小根堆
scanf("%d%d%d%d%d%d", &ex, &ey, &sx, &sy, &tx, &ty);
if(sx == tx && sy == ty)//他本来就在目标位置
{
printf("0\n");
return;
}
memset(di, 0x3f, sizeof(di));//初始化距离数组
memset(v, 0, sizeof(v));//初始化
mp[sx][sy] = 0;///注意要把指定可移动块标记为不可移动
for (int i = 0; i <= 3; i++)//枚举空白格子去指定可移动块的那个方向
{
int nx = sx + dx[i], ny = sy + dy[i];
if (valid(nx, ny))//这个位置合法
{
int ds = dis(ex, ey, nx, ny);//计算距离
pq.push(st(sx, sy, i, ds));//扔进小根堆,dij用
di[sx][sy][i] = ds;//更新dijkstra的di数组
}
}
mp[sx][sy] = 1;//把指定可移动块不可移动的标记还原
while (!pq.empty())//dijkstra的套路
{
st now = pq.top();
pq.pop();
// printf("迪杰斯特拉 %d %d (%d,%d) %d\n", now.x, now.y, dx[now.d], dy[now.d], now.dis);
if (v[now.x][now.y][now.d] == 1)
continue;
v[now.x][now.y][now.d] = 1;
int &x = now.x, &y = now.y;
for (int i = 0; i <= 3; i++)
{
int nx = x + dx[i], ny = y + dy[i];//让空白块移动到(nx,ny)然后让指定可移动块移动到空白块位置
// printf("下一个为(%d,%d)\n", nx, ny);
if (valid(nx, ny))//(nx,ny)是合法的
{
// printf("(%d,%d)合法\n", nx, ny);
int ds = tt[x][y][now.d][i];//直接从tt数组获取空白格子移动的距离
if (v[nx][ny][rev(i)] == 0 && now.dis + ds + 1 < di[nx][ny][rev(i)])//dij套路,更新距离
{
// printf("由(%d,%d,%d,%d,%d)到(%d,%d,%d,%d,%d)\n", now.x, now.y, dx[now.d], dy[now.d], now.dis, nx, ny, dx[rev(i)], dy[rev(i)], now.dis + ds + 1);
di[nx][ny][rev(i)] = now.dis + ds + 1;
pq.push(st(nx, ny, rev(i), now.dis + ds + 1));
}
}
}
}
int mind = inf;
for (int i = 0; i <= 3; i++)//枚举目标位置的4个方向的状态更新最小值
{
mind = min(mind, di[tx][ty][i]);
// printf("di[%d][%d][%d] = %d\n", tx, ty, i, di[tx][ty][i]);
}
if (mind == inf)//最小值没有被更新,说明目标位置不可到达
printf("-1\n");
else
printf("%d\n", mind);
}
//主函数
int main()
{
scanf("%d%d%d", &n, &m, &q);
for (int i = 1; i <= n; i++)
for (int j = 1; j <= m; j++)
scanf("%d", &mp[i][j]);
prework();
for (int i = 1; i <= q; i++)
work();
return 0;
}